ECE 280/Imaging Lab 1

This page serves as a supplement to the first Digital Image Processing Lab for ECE 280.

Corrections / Clarifications to the Handout

You will need the Image Processing Toolbox; if you do not have it, there is information below on how to install it.

Running MATLAB

MATLAB can be run remotely on the Duke Linux system, but it will generally be more convenient for you to install it on your own computer. All the documentation for this lab was written using MATLAB R2020a and tested with MATLAB R2021a. It is likely that MATLAB R2020b will also work. Previous versions of MATLAB have not been tested.

Note: Evelyn (a previous Head TA) discovered that at least MATLAB 2018a uses 64 levels instead of 256 levels by default. If you are using an earlier version of MATLAB, when you create a colormap, you may need to write colormap gray(256) instead of just colormap gray in examples 2 and 8 and exercise 7 specifically.

Installing MATLAB

MATLAB is free for Duke students. Follow the instructions in the Installation section of the EGRWiki page on MATLAB. Be sure to select the appropriate PRODUCTS when asked.

Adding the Image Processing Toolbox

If you installed MATLAB on your own computer but do not have the Image Processing Toolbox:

Go to the HOME tab in MATLAB
Find and click on "Add-Ons"
Search for Image Processing
Click on the link for the Image Processing Toolbox
Sign in to install if need be
Install

Image Processing Toolbox

For this lab, there are a few commands you will need to learn (or remember):

imread('filename.ext') will load an image into MATLAB. Depending on the image type, the return from this function may be a matrix of binary numbers (black and white images), an array of integers between 0 and 255 (grayscale images), or a three-layer matrix of integers between 0 and 255 (color images).
image(matrix) will display the contents of a matrix as viewed from above.
- By default, the image command for a 1-layer matrix will assign colors based on a colormap that spans values from 0 to 255. Anything outside of that range will be clipped.
- There are ways to change that, but you will not need to for this lab
- The image command for a 3-layer matrix will assign colors based on the first layer being the red component, the second layer being the green component, and the third layer being the blue component.
  - If the matrix is made up of floating-point numbers, image expects those numbers to be in the range [0, 1]
  - If the matrix is made up of unsigned integers, image expects those numbers to be in the range [0, 255]
  - If the matrix is made up of signed integers, image expects those numbers to be in the range [-128, 127]
imagesc(matrix) for a one layer matrix will display the contents of a matrix as viewed from above and will also map the minimum value to "color 0" and the maximum value to "color 255"; for a three-layer matrix it will work just like image
imagesc(matrix, [c_low c_high) for a one layer matrix will display the contents of a matrix as viewed from above and will also map the colors c_low and below to "color 0" and colors c_high and above to "color 255"; the colors in between will be linearly mapped to the colormap.
colorbar will add a...colorbar to the right of an image to show the numerical values and colors associated with them. This is only useful for a one-layer image.
colormap MAP will assign a particular colormap. For this assignment, the most useful one is gray for grayscale images.
axis equal will tell MATLAB to display an item such that each direction has the same scale. For the imaging commands, this is useful in that it will make each pixel a square regardless of the shape of the figure window, thus preserving the geometry of an image.

Links

2D Convolution link for 6.1: https://www.songho.ca/dsp/convolution/convolution2d_example.html
Kernel link for Exercise 7: https://en.wikipedia.org/wiki/Kernel_(image_processing)
Test Card for Exercise 8: https://en.wikipedia.org/wiki/Test_card

Examples

The following sections will contain both the example programs given in the lab as well as the image or images they produce. You should still type these into your own version of MATLAB to make sure you are getting the same answers. These are provided so you can compare what you get with what we think you should get.

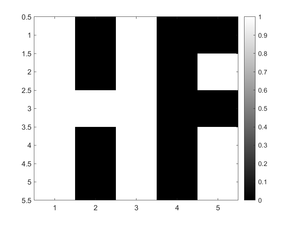
Example 1: Black & White Images

a = [ 1 0 1 0 0; ...
      1 0 1 0 1; ...
      1 1 1 0 0; ...
      1 0 1 0 1; ...
      1 0 1 0 1 ];
figure(1); clf
imagesc(a)
colormap gray; colorbar

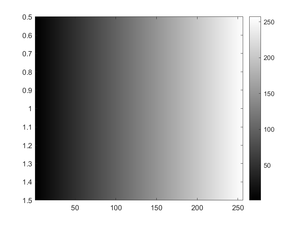
Example 2: Simple Grayscale Images

b = 0:255;
figure(1); clf
image(b) 
colormap gray; colorbar

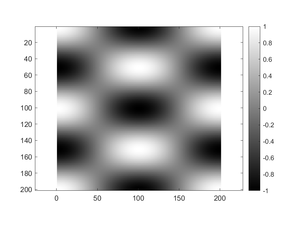
Example 3: Less Simple Grayscale Images

[x, y] = meshgrid(linspace(0, 2*pi, 201));
z = cos(x).*cos(2*y);
figure(1); clf
imagesc(z)
axis equal; colormap gray; colorbar

Notice how the use of axis equal made the image look like a square since it is 201x201 but also caused the display to be filled with whitespace as a result of the figure size versus the image size.

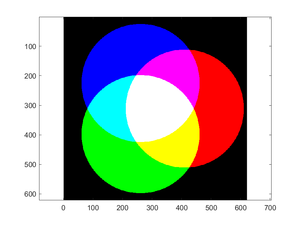
Example 4: Building an Image

rad = 100;
del = 10;
[x, y] = meshgrid((-3*rad-del):(3*rad+del));
[rows, cols] = size(x);
dist = @(x, y, xc, yc) sqrt((x-xc).^2+(y-yc).^2);
venn_img = zeros(rows, cols, 3);
venn_img(:,:,1) = (dist(x, y, rad.*cos(0), rad.*sin(0)) < 2*rad);
venn_img(:,:,2) = (dist(x, y, rad.*cos(2*pi/3), rad.*sin(2*pi/3)) < 2*rad);
venn_img(:,:,3) = (dist(x, y, rad.*cos(4*pi/3), rad.*sin(4*pi/3)) < 2*rad);
figure(1); clf
image(venn_img)
axis equal

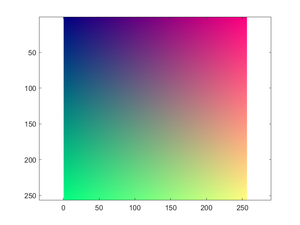
Example 5: Exploring Colors

[x, y] = meshgrid(linspace(0, 1, 256));
other = 0.5;
palette = zeros(256, 256, 3);
palette(:,:,1) = x;
palette(:,:,2) = y;
palette(:,:,3) = other;
figure(1); clf
imagesc(palette)
axis equal

Example 6: 1D Convolution

x = [1, 2, 4, 8, 7, 5, 1]
h = [1, -1]
y = conv(x, h)

x =

     1     2     4     8     7     5     1


h =

     1    -1


y =

     1     1     2     4    -1    -2    -4    -1

Example 7: 1D Convolution Using 'same'

x = [1, 2, 4, 8, 7, 5, 1]
h = [1, -1]
y = conv(x, h, 'same')

x =

     1     2     4     8     7     5     1


h =

     1    -1


y =

     1     2     4    -1    -2    -4    -1

Example 8: 10x10 Blurring

x = imread('coins.png');
h = ones(10, 10)/10^2;
y = conv2(x, h, 'same');
figure(1); clf
image(x)
axis equal; colormap gray; colorbar
title('Original')
figure(2); clf
image(y)
axis equal; colormap gray; colorbar
title('10x10 Blur')

Example 9: Make No Assumptions

x = [1, 2, 4, 8, 7, 5, 1]
h = [1, -1]
y = conv(x, h, 'valid')

x =

     1     2     4     8     7     5     1


h =

     1    -1


y =

     1     2     4    -1    -2    -4

Example 10: Basic Edge Detection and Display

[x, y] = meshgrid(linspace(-1, 1, 200));
z1 = (.7<sqrt(x.^2+y.^2)) & (sqrt(x.^2+y.^2)<.9);
z2 = (.3<sqrt(x.^2+y.^2)) & (sqrt(x.^2+y.^2)<.5);
zimg = 100*z1+200*z2;
figure(1); clf
image(zimg); 
axis equal; colormap gray; colorbar; title('Original')

hx = [1 -1; 1 -1];
edgex = conv2(zimg, hx, 'valid');
figure(2); clf
imagesc(edgex, [-512, 512]); 
axis equal; colormap gray; colorbar; title('Vertical Edges')

hy = hx';
edgey = conv2(zimg, hy, 'valid');
figure(3); clf
imagesc(edgey, [-512, 512]); 
axis equal; colormap gray; colorbar; title('Horizontal Edges')

edges = sqrt(edgex.^2 + edgey.^2);
figure(4); clf
imagesc(edges); 
axis equal; colormap gray; colorbar; title('Edges')

Original
Vertical Edges
Horizontal Edges
Edges

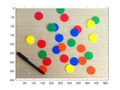
Example 11: Chips!

clear
img = imread('coloredChips.png');
figure(1); clf
title('Original')
image(img); axis equal
vals = (0:255)'/255;
names = {'Red', 'Green', 'Blue'}
for k = 1:3
    figure(k+1); clf
    image(img(:,:,k)); axis equal
    colormap gray; colorbar
    title(names{k}+" as Gray")
    figure(k+4)
    image(img(:,:,k)); axis equal
    cmap = zeros(256, 3);
    cmap(:,k) = vals;
    colormap(cmap); colorbar
    title(names{k}+" as "+names{k})
end

Original

Red as Gray
Green as Gray
Blue as Gray

Red as Red
Green as Green
Blue as Blue

Example 12: Chip Edges!

clear
img = imread('coloredChips.png');
figure(1); clf
image(img); axis equal

h = [1 0 -1; 2 0 -2; 1 0 -1]
for k=1:3
    y(:,:,k) = conv2(img(:,:,k), h, 'valid');
    figure(1+k); clf
    imagesc(y(:,:,k), [-1020, 1020]); 
    axis equal; colormap gray; colorbar
    figure(4+k); clf
    imagesc(abs(y(:,:,k)), [0, 1020]); 
    axis equal; colormap gray; colorbar
end
%%
yx = (y+max(abs(y(:)))) / 2 / max(abs(y(:)));
figure(8); clf
image(yx); axis equal

yg = sqrt(y(:,:,1).^2 + y(:,:,2).^2 + y(:,:,3).^2);
ygs = abs(yg) / max(yg(:)) * 255;
figure(9); clf
image(ygs); colormap gray; axis equal

Original

Red Edges as Gray
Green Edges as Gray
Blue Edges as Gray

Absolute Red Edges as Gray
Absolute Green Edges as Gray
Absolute Blue Edges as Gray

Colorful Edges
Absolute Edges

Exercise Starter Codes

Exercise 3

tc = linspace(0, 1, 101);
xc = humps(tc);
td = linspace(0, 1, 11);
xd = humps(td);
figure(1); clf
plot(tc, xc, 'b-')
hold on
plot(td, xd, 'bo')
hold off

Exercise 4

tc = linspace(0, 1, 101);
xc = humps(tc);
deltatc = tc(2)-tc(1);
td = linspace(0, 1, 11);
xd = humps(td);
deltatd = td(2)-td(1);

figure(1); clf
plot(tc, xc, 'b-')
hold on
plot(td, xd, 'bo')
hold off
title('Values')

figure(2); clf
twopointdiff = diff(xc)/deltatc;
twopointdiff(end+1)=twopointdiff(end);
plot(tc, twopointdiff, 'b-')
hold on
plot(tc(1:10:end), twopointdiff(1:10:end), 'bo')
hold off
title('Change Me')

ECE 280/Imaging Lab 1

Contents