Difference between revisions of "ECE 280/Imaging Lab 2"

From PrattWiki
Jump to navigation Jump to search
(→‎Example 5: MATLAB fft2 and ifft2 for Even Dimensions)
 
(7 intermediate revisions by the same user not shown)
Line 1: Line 1:
−
This page serves as a supplement to the second Digital Image Processing Labs for ECE 280.  It has been updated for the Spring 2021 semester.  This worksheet assumes you have done everything necessary to successfully complete [[ECE 280/Imaging Lab 1 | Imaging Lab 1]], including working with MATLAB and understanding basic image processing commands in MATLAB.
+
This page serves as a supplement to the second Digital Image Processing Labs for ECE 280.  This worksheet assumes you have done everything necessary to successfully complete [[ECE 280/Imaging Lab 1 | Imaging Lab 1]], including working with MATLAB and understanding basic image processing commands in MATLAB.
  
 
== Corrections / Clarifications to the Handout ==
 
== Corrections / Clarifications to the Handout ==
Line 12: Line 12:
  
 
=== Example 1: Signal Analysis ===
 
=== Example 1: Signal Analysis ===
−
Since the point of Exercise 1 is to write the code to perform the calculations in this example, we'l.. just move right along to...
+
Since the point of Exercise 1 is to write the code to perform the calculations in this example, we'll.. just move right along to...
−
 
 
−
 
 
  
 
=== Example 2: MATLAB fft ===
 
=== Example 2: MATLAB fft ===
Line 171: Line 169:
 
<gallery>
 
<gallery>
 
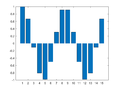
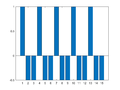
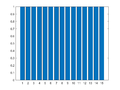
File:IP2 E4a Plot1.png|Xm=[15, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
 
File:IP2 E4a Plot1.png|Xm=[15, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
−
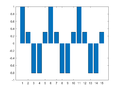
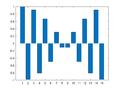
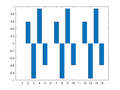
File:IP2 E4a Plot2.png|Xm=[0, 7.5, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 7.5]
+
File:IP2 E4a Plot2.png|Xm=[0, 7.5/j, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -7.5/j]
−
File:IP2 E4a Plot3.png|Xm=[0, 0, 7.5, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 7.5, 0]
+
File:IP2 E4a Plot3.png|Xm=[0, 0, 7.5/j, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -7.5/j, 0]
−
File:IP2 E4a Plot4.png|Xm=[0, 0, 0, 7.5, 0, 0, 0, 0, 0, 0, 0, 0, 7.5, 0, 0]
+
File:IP2 E4a Plot4.png|Xm=[0, 0, 0, 7.5/j, 0, 0, 0, 0, 0, 0, 0, 0, -7.5/j, 0, 0]
 
</gallery>
 
</gallery>
 
<gallery>
 
<gallery>
−
File:IP2 E4a Plot5.png|Xm=[0, 0, 0, 0, 7.5, 0, 0, 0, 0, 0, 0, 7.5, 0, 0, 0]
+
File:IP2 E4a Plot5.png|Xm=[0, 0, 0, 0, 7.5/j, 0, 0, 0, 0, 0, 0, -7.5/j, 0, 0, 0]
−
File:IP2 E4a Plot6.png|Xm=[0, 0, 0, 0, 0, 7.5, 0, 0, 0, 0, 7.5, 0, 0, 0, 0]
+
File:IP2 E4a Plot6.png|Xm=[0, 0, 0, 0, 0, 7.5/j, 0, 0, 0, 0, -7.5/j, 0, 0, 0, 0]
−
File:IP2 E4a Plot7.png|Xm=[0, 0, 0, 0, 0, 0, 7.5, 0, 0, 7.5, 0, 0, 0, 0, 0]
+
File:IP2 E4a Plot7.png|Xm=[0, 0, 0, 0, 0, 0, 7.5/j, 0, 0, -7.5/j, 0, 0, 0, 0, 0]
−
File:IP2 E4a Plot8.png|Xm=[0, 0, 0, 0, 0, 0, 0, 7.5, 7.5, 0, 0, 0, 0, 0, 0]
+
File:IP2 E4a Plot8.png|Xm=[0, 0, 0, 0, 0, 0, 0, 7.5/j, -7.5/j, 0, 0, 0, 0, 0, 0]
 
</gallery>
 
</gallery>
−
 
  
 
=== Example 5: MATLAB fft2 and ifft2 for Even Dimensions ===
 
=== Example 5: MATLAB fft2 and ifft2 for Even Dimensions ===
Line 220: Line 217:
 
<br clear=all>
 
<br clear=all>
 
where the matching colors denote the requisite complex conjugate pairs.
 
where the matching colors denote the requisite complex conjugate pairs.
 +
 +
=== Example 6: FFT of Coins ===
 +
<syntaxhighlight lang=matlab>
 +
x = imread('coins.png');
 +
x = x(2:end, 2:end);
 +
figure(1); clf
 +
image(x); axis equal; colormap gray; colorbar
 +
X = fft2(x);
 +
Xs = fftshift(X);
 +
figure(2); clf
 +
imagesc(abs(X)); axis equal; colormap gray; colorbar
 +
figure(3); clf
 +
imagesc(abs(Xs)); axis equal; colormap gray; colorbar
 +
figure(4); clf
 +
imagesc(log10(abs(Xs))); axis equal; colormap gray; colorbar
 +
 +
Xnodc = fft2(x); Xnodc(1,1) = 0;
 +
Xnodcs = fftshift(Xnodc);
 +
figure(5); clf
 +
imagesc(abs(Xnodcs)); axis equal; colormap gray; colorbar
 +
figure(6); clf
 +
imagesc(log10(abs(Xnodcs))); axis equal; colormap gray; colorbar
 +
</syntaxhighlight>
 +
 +
<br clear=all>
 +
<gallery>
 +
File:IP2 E6 Plot1.png| Original
 +
File:IP2 E6 Plot2.png| Magnitude of fft
 +
File:IP2 E6 Plot3.png| Shifted Magnitude
 +
File:IP2 E6 Plot4.png| log of Shifted Magnitude
 +
File:IP2 E6 Plot5.png| Shifted Magnitude sans DC
 +
File:IP2 E6 Plot6.png| log of Shifted Magnitude sans DC
 +
</gallery>
 +
 +
=== Example 7: Round LPF Applied to Coins ===
 +
<syntaxhighlight lang=matlab>
 +
x = imread('coins.png');
 +
x = x(2:end, 2:end);
 +
figure(1); clf
 +
image(x); axis equal; colormap gray; colorbar
 +
 +
X = fft2(x);
 +
Xs = fftshift(X);
 +
figure(2); clf
 +
imagesc(log10(abs(Xs))); axis equal; colormap gray; colorbar
 +
 +
[rows, cols] = size(x);
 +
max_size = max(rows, cols);
 +
rnorm = rows/max_size; cnorm = cols/max_size;
 +
[v, u] = meshgrid(linspace(-cnorm, cnorm, cols),...
 +
    linspace(-rnorm, rnorm, rows)) ;
 +
filter = sqrt(u.^2+v.^2)<0.5;
 +
figure(3); clf
 +
imagesc(filter); axis equal; colormap gray; colorbar
 +
 +
Xsfiltered = Xs.*filter;
 +
figure(4); clf
 +
imagesc(log10(abs(Xsfiltered))); axis equal; colormap gray; colorbar
 +
 +
Xfiltered = ifftshift(Xsfiltered);
 +
xfiltered = ifft2(Xfiltered);
 +
figure(5); clf
 +
imagesc(xfiltered, [0, 255]); axis equal; colormap gray; colorbar
 +
</syntaxhighlight>
 +
 +
<br clear=all>
 +
<gallery>
 +
File:IP2 E7 Plot1.png| Original
 +
File:IP2 E7 Plot2.png| log of Shifted Magnitude
 +
File:IP2 E7 Plot3.png| Filter Magnitude
 +
File:IP2 E7 Plot4.png| log of Filtered Shifted Magnitude
 +
File:IP2 E7 Plot5.png| Filtered Image
 +
</gallery>
 +
 +
=== Example 8: Rectangular LPF Applied to Coins ===
 +
<syntaxhighlight lang=matlab>
 +
x = imread('coins.png');
 +
x = x(2:end, 2:end);
 +
figure(1); clf
 +
image(x); axis equal; colormap gray; colorbar
 +
 +
X = fft2(x);
 +
Xs = fftshift(X);
 +
figure(2); clf
 +
imagesc(log10(abs(Xs))); axis equal; colormap gray; colorbar
 +
 +
[rows, cols] = size(x);
 +
max_size = max(rows, cols);
 +
rnorm = rows/max_size; cnorm = cols/max_size;
 +
[v, u] = meshgrid(linspace(-cnorm, cnorm, cols),...
 +
    linspace(-rnorm, rnorm, rows)) ;
 +
filter = (abs(u)<0.5) & (abs(v)<0.5);
 +
figure(3); clf
 +
imagesc(filter); axis equal; colormap gray; colorbar
 +
 +
Xsfiltered = Xs.*filter;
 +
figure(4); clf
 +
imagesc(log10(abs(Xsfiltered))); axis equal; colormap gray; colorbar
 +
 +
Xfiltered = ifftshift(Xsfiltered);
 +
xfiltered = ifft2(Xfiltered);
 +
figure(5); clf
 +
imagesc(xfiltered, [0, 255]); axis equal; colormap gray; colorbar
 +
</syntaxhighlight>
 +
 +
<br clear=all>
 +
<gallery>
 +
File:IP2 E8 Plot1.png| Original
 +
File:IP2 E8 Plot2.png| log of Shifted Magnitude
 +
File:IP2 E8 Plot3.png| Filter Magnitude
 +
File:IP2 E8 Plot4.png| log of Filtered Shifted Magnitude
 +
File:IP2 E8 Plot5.png| Filtered Image
 +
</gallery>
 +
 +
=== Example 9: Rectangular HPF Applied to Coins ===
 +
<syntaxhighlight lang=matlab>
 +
x = imread('coins.png');
 +
x = x(2:end, 2:end);
 +
figure(1); clf
 +
image(x); axis equal; colormap gray; colorbar
 +
 +
X = fft2(x);
 +
Xs = fftshift(X);
 +
figure(2); clf
 +
imagesc(log10(abs(Xs))); axis equal; colormap gray; colorbar
 +
 +
[rows, cols] = size(x);
 +
max_size = max(rows, cols);
 +
rnorm = rows/max_size; cnorm = cols/max_size;
 +
[v, u] = meshgrid(linspace(-cnorm, cnorm, cols),...
 +
    linspace(-rnorm, rnorm, rows)) ;
 +
filter = (abs(u)>0.1) | (abs(v)>0.1);
 +
figure(3); clf
 +
imagesc(filter); axis equal; colormap gray; colorbar
 +
 +
Xsfiltered = Xs.*filter;
 +
figure(4); clf
 +
imagesc(log10(abs(Xsfiltered))); axis equal; colormap gray; colorbar
 +
 +
Xfiltered = ifftshift(Xsfiltered);
 +
xfiltered = ifft2(Xfiltered);
 +
figure(5); clf
 +
imagesc(xfiltered); axis equal; colormap gray; colorbar
 +
</syntaxhighlight>
 +
 +
<br clear=all>
 +
<gallery>
 +
File:IP2 E9 Plot1.png| Original
 +
File:IP2 E9 Plot2.png| log of Shifted Magnitude
 +
File:IP2 E9 Plot3.png| Filter Magnitude
 +
File:IP2 E9 Plot4.png| log of Filtered Shifted Magnitude
 +
File:IP2 E9 Plot5.png| Filtered Image
 +
</gallery>
 +
  
 
<!--
 
<!--
Line 465: Line 616:
 
</syntaxhighlight>
 
</syntaxhighlight>
 
-->
 
-->
 +
[[Category:ECE 280]]

Latest revision as of 21:15, 2 May 2023

This page serves as a supplement to the second Digital Image Processing Labs for ECE 280. This worksheet assumes you have done everything necessary to successfully complete Imaging Lab 1, including working with MATLAB and understanding basic image processing commands in MATLAB.

Corrections / Clarifications to the Handout

  • None yet


Links

Examples

The following sections will contain both the example programs given in the lab as well as the image or images they produce. You should still type these into your own version of MATLAB to make sure you are getting the same answers. These are provided so you can compare what you get with what we think you should get.

Example 1: Signal Analysis

Since the point of Exercise 1 is to write the code to perform the calculations in this example, we'll.. just move right along to...

Example 2: MATLAB fft

x = [1, 5, 2, 3, 1]
X = fft(x)

yields 

[12.0000 + 0.0000i, -1.1910 - 3.2164i, -2.3090 - 3.3022i, -2.3090 + 3.3022i, -1.1910 + 3.2164i


Example 3: MATLAB fft2 and ifft2

clear
x1 = [1, 1; 1, 1]
x2 = [1, 1; 0, 0]
x3 = [1, 0; 1, 0]
x4 = [1, 0; 0, 1]

X1=fft2(x1)
X2=fft2(x2)
X3=fft2(x3)
X4=fft2(x4)

x1a = ifft2(X1)
x2a = ifft2(X2)
x3a = ifft2(X3)
x4a = ifft2(X4)

yields: 

x1 =

     1     1
     1     1


x2 =

     1     1
     0     0


x3 =

     1     0
     1     0


x4 =

     1     0
     0     1


X1 =

     4     0
     0     0


X2 =

     2     0
     2     0


X3 =

     2     2
     0     0


X4 =

     2     0
     0     2


x1a =

     1     1
     1     1


x2a =

     1     1
     0     0


x3a =

     1     0
     1     0


x4a =

     1     0
     0     1


Example 4: One-Dimensional Frequency Mapping

M = 15;
for m=0:((M+1)/2-1)
    Xm = zeros(M,1);
    Xm(m+1) = M/2;
    if m==0
        Xm(m+1)= M;  
    else
        Xm(M+1-m) = M/2;
    end
    x = ifft(Xm);
    figure(m+1); clf
    bar(x)
end


  • Xm=[15, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

  • Xm=[0, 7.5, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 7.5]

  • Xm=[0, 0, 7.5, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 7.5, 0]

  • Xm=[0, 0, 0, 7.5, 0, 0, 0, 0, 0, 0, 0, 0, 7.5, 0, 0]

  • Xm=[0, 0, 0, 0, 7.5, 0, 0, 0, 0, 0, 0, 7.5, 0, 0, 0]

  • Xm=[0, 0, 0, 0, 0, 7.5, 0, 0, 0, 0, 7.5, 0, 0, 0, 0]

  • Xm=[0, 0, 0, 0, 0, 0, 7.5, 0, 0, 7.5, 0, 0, 0, 0, 0]

  • Xm=[0, 0, 0, 0, 0, 0, 0, 7.5, 7.5, 0, 0, 0, 0, 0, 0]

Example 4a: One-Dimensional Frequency Mapping (Odd Symmetry)

M = 15;
for m=0:((M+1)/2-1)
    Xm = zeros(M,1);
    Xm(m+1) = M/2/j;
    if m==0
        Xm(m+1)= M;  
    else
        Xm(M+1-m) = -M/2/j;
    end
    x = ifft(Xm);
    figure(m+1); clf
    bar(x)
end


  • Xm=[15, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]

  • Xm=[0, 7.5/j, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -7.5/j]

  • Xm=[0, 0, 7.5/j, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, -7.5/j, 0]

  • Xm=[0, 0, 0, 7.5/j, 0, 0, 0, 0, 0, 0, 0, 0, -7.5/j, 0, 0]

  • Xm=[0, 0, 0, 0, 7.5/j, 0, 0, 0, 0, 0, 0, -7.5/j, 0, 0, 0]

  • Xm=[0, 0, 0, 0, 0, 7.5/j, 0, 0, 0, 0, -7.5/j, 0, 0, 0, 0]

  • Xm=[0, 0, 0, 0, 0, 0, 7.5/j, 0, 0, -7.5/j, 0, 0, 0, 0, 0]

  • Xm=[0, 0, 0, 0, 0, 0, 0, 7.5/j, -7.5/j, 0, 0, 0, 0, 0, 0]

Example 5: MATLAB fft2 and ifft2 for Even Dimensions

x1 = [3, 4, 5, 7; 9, 7, 5, 3; 1, 8, 6, 7; 4, 2, 7, 6]
X1 = fft2(x1)

yields

$$ \begin{align*} X1 &= \begin{bmatrix} 84 & \color{Red}{-6+2j} & -4 & \color{Red}{-6-2j}\\ \color{Orange}{-3-5j} & \color{Green}{-5-3j} & \color{Blue}{5-1j} & \color{Orchid}{11-11j}\\ -2 & \color{Brown}{-8+2j} & -18 & \color{Brown}{-8-2j}\\ \color{Orange}{-3+5j} & \color{Orchid}{11+11j} & \color{Blue}{5+1j} & \color{Green}{-5+3j} \end{bmatrix} \end{align*} $$

and 

fftshift(X1)

yields

$$ \begin{align*} \begin{bmatrix} -18 & \color{Brown}{-8-2j} & -2 & \color{Brown}{-8+2j} \\ \color{Blue}{5+1j} & \color{Green}{-5+3j} & \color{Orange}{-3+5j} & \color{Orchid}{11+11j}\\ -4 & \color{Red}{-6-2j} & 84 & \color{Red}{-6+2j}\\ \color{Blue}{5-1j} & \color{Orchid}{11-11j} & \color{Orange}{-3-5j} & \color{Green}{-5-3j}\\ \end{bmatrix} \end{align*} $$


where the matching colors denote the requisite complex conjugate pairs.

Example 6: FFT of Coins

x = imread('coins.png');
x = x(2:end, 2:end);
figure(1); clf
image(x); axis equal; colormap gray; colorbar
X = fft2(x);
Xs = fftshift(X);
figure(2); clf
imagesc(abs(X)); axis equal; colormap gray; colorbar
figure(3); clf
imagesc(abs(Xs)); axis equal; colormap gray; colorbar
figure(4); clf
imagesc(log10(abs(Xs))); axis equal; colormap gray; colorbar

Xnodc = fft2(x); Xnodc(1,1) = 0;
Xnodcs = fftshift(Xnodc);
figure(5); clf
imagesc(abs(Xnodcs)); axis equal; colormap gray; colorbar
figure(6); clf
imagesc(log10(abs(Xnodcs))); axis equal; colormap gray; colorbar


  • Original

  • Magnitude of fft

  • Shifted Magnitude

  • log of Shifted Magnitude

  • Shifted Magnitude sans DC

  • log of Shifted Magnitude sans DC

Example 7: Round LPF Applied to Coins

x = imread('coins.png');
x = x(2:end, 2:end);
figure(1); clf
image(x); axis equal; colormap gray; colorbar

X = fft2(x);
Xs = fftshift(X);
figure(2); clf
imagesc(log10(abs(Xs))); axis equal; colormap gray; colorbar

[rows, cols] = size(x);
max_size = max(rows, cols);
rnorm = rows/max_size; cnorm = cols/max_size;
[v, u] = meshgrid(linspace(-cnorm, cnorm, cols),...
    linspace(-rnorm, rnorm, rows)) ;
filter = sqrt(u.^2+v.^2)<0.5;
figure(3); clf
imagesc(filter); axis equal; colormap gray; colorbar

Xsfiltered = Xs.*filter;
figure(4); clf
imagesc(log10(abs(Xsfiltered))); axis equal; colormap gray; colorbar

Xfiltered = ifftshift(Xsfiltered);
xfiltered = ifft2(Xfiltered);
figure(5); clf
imagesc(xfiltered, [0, 255]); axis equal; colormap gray; colorbar


  • Original

  • log of Shifted Magnitude

  • Filter Magnitude

  • log of Filtered Shifted Magnitude

  • Filtered Image

Example 8: Rectangular LPF Applied to Coins

x = imread('coins.png');
x = x(2:end, 2:end);
figure(1); clf
image(x); axis equal; colormap gray; colorbar

X = fft2(x);
Xs = fftshift(X);
figure(2); clf
imagesc(log10(abs(Xs))); axis equal; colormap gray; colorbar

[rows, cols] = size(x);
max_size = max(rows, cols);
rnorm = rows/max_size; cnorm = cols/max_size;
[v, u] = meshgrid(linspace(-cnorm, cnorm, cols),...
    linspace(-rnorm, rnorm, rows)) ;
filter = (abs(u)<0.5) & (abs(v)<0.5);
figure(3); clf
imagesc(filter); axis equal; colormap gray; colorbar

Xsfiltered = Xs.*filter;
figure(4); clf
imagesc(log10(abs(Xsfiltered))); axis equal; colormap gray; colorbar

Xfiltered = ifftshift(Xsfiltered);
xfiltered = ifft2(Xfiltered);
figure(5); clf
imagesc(xfiltered, [0, 255]); axis equal; colormap gray; colorbar


  • Original

  • log of Shifted Magnitude

  • Filter Magnitude

  • log of Filtered Shifted Magnitude

  • Filtered Image

Example 9: Rectangular HPF Applied to Coins

x = imread('coins.png');
x = x(2:end, 2:end);
figure(1); clf
image(x); axis equal; colormap gray; colorbar

X = fft2(x);
Xs = fftshift(X);
figure(2); clf
imagesc(log10(abs(Xs))); axis equal; colormap gray; colorbar

[rows, cols] = size(x);
max_size = max(rows, cols);
rnorm = rows/max_size; cnorm = cols/max_size;
[v, u] = meshgrid(linspace(-cnorm, cnorm, cols),...
    linspace(-rnorm, rnorm, rows)) ;
filter = (abs(u)>0.1) | (abs(v)>0.1);
figure(3); clf
imagesc(filter); axis equal; colormap gray; colorbar

Xsfiltered = Xs.*filter;
figure(4); clf
imagesc(log10(abs(Xsfiltered))); axis equal; colormap gray; colorbar

Xfiltered = ifftshift(Xsfiltered);
xfiltered = ifft2(Xfiltered);
figure(5); clf
imagesc(xfiltered); axis equal; colormap gray; colorbar


  • Original

  • log of Shifted Magnitude

  • Filter Magnitude

  • log of Filtered Shifted Magnitude

  • Filtered Image

Retrieved from "https://pundit.pratt.duke.edu/piki/index.php?title=ECE_280/Imaging_Lab_2&oldid=29832"