Maple/Plotting
Maple has several built in commands to make plots. This page will show you how to use the {\tt plot} command.
Basics
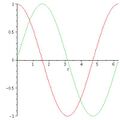
The command generally takes at least two arguments - an array of items to plot and a statement about the independent variable and its values. For example, to plot cos and sin over one period, you could type:
plot([cos(t), sin(t)], t = 0 .. 2*Pi)
If you have a variable that has several unknowns, you can use the
subs command to make substitutions for all but the independent
variable of the plot. For example, given some function \(f\):
which can be defined in Maple using the code:
f:=exp(-t)*cos(omega*t-k*x)
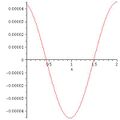
and assuming \(\omega\) is known to be 5 rad/s and \(k\) is 3 rad/m, you could make a plot of \(f\) at \(t=10\) s over the course of a 2 m section:
FVals:= omega=5, k=3;
plot(subs(FVals, t=10, f), x=0..2)
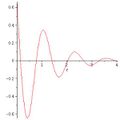
With the same equation, then, you could make a plot of \(f\) at the 6 m mark for times between 0 and 4 just by switching the variables around a bit:
FVals:= omega=5, k=3;
plot(subs(FVals, x=6, f), t=0..4)
Simple plotting example
Plot of \(e^{-10}\cos(50-3x)\)
Plot of \(e^{-t}\cos(5t-12)\)
Plot Options
There are several plot options, which are described in the help file
for plot as well as a help file for plot options. The main ones to
use here will be the labels, labeldirections, title,
and legend. Options
go after the independent argument and are separated by commas. For
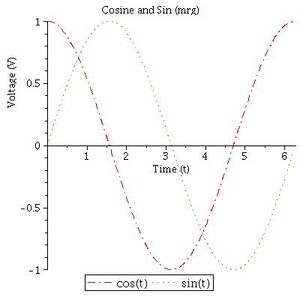
example, a more complete version of the trig plot above might be:
plot([cos(t), sin(t)], t = 0 .. 2*Pi,
labels = ["Time (t)", "Voltage (V)"],
labeldirections = [horizontal, vertical],
title = "Cosine and Sin (mrg)",
legend = ["cos(t)", "sin(t)"])
Note - using Shift-Enter will go to a new line.
Plotting Functions with Vestigial Imaginary Parts =
Oftentimes, solving differential equations or inverse Laplace transforms will yield small roundoff errors that cause a function which should be purely real to have a vestigial imaginary component. To eliminate this - and thus make it possible to see the plot - use Maple's map command to apply the Re command to your function.
