Difference between revisions of "ECE 280/PlotDemo"
Jump to navigation
Jump to search
| Line 6: | Line 6: | ||
% MATLAB and Maple Demo | % MATLAB and Maple Demo | ||
% M. R. Gustafson II | % M. R. Gustafson II | ||
| − | |||
%% Initialize | %% Initialize | ||
| Line 12: | Line 11: | ||
%% Define step and ramp functions | %% Define step and ramp functions | ||
| − | + | ustep = @(in) (1.0).*(in>=0); | |
| − | + | uramp = @(in) (in).*(in>=0); | |
%% Define x and y using accumulation | %% Define x and y using accumulation | ||
| − | X = @(t) (-1)* | + | X = @(t) (-1)*uramp(t+1)+ustep(t)+(2)*uramp(t)+(-1)*uramp(t-1)+(-1)*uramp(t-2)+(1)*uramp(t-3); |
| − | Y = @(t) | + | Y = @(t) ustep(t+2)+(-2)*ustep(t+1)+uramp(t)+(-1)*uramp(t-1)+ustep(t-1)-ustep(t-2); |
%% Plot signals | %% Plot signals | ||
| Line 25: | Line 24: | ||
t, Y(t), 'b:', ... | t, Y(t), 'b:', ... | ||
t, X(t).*Y(t), 'g--') | t, X(t).*Y(t), 'g--') | ||
| − | legend('x(t)', 'y(t)', 'x(t) y(t)', | + | legend('x(t)', 'y(t)', 'x(t) y(t)', 'location','best') |
xlabel('t') | xlabel('t') | ||
gzoom | gzoom | ||
| Line 39: | Line 38: | ||
t, IntY(t), 'b:', ... | t, IntY(t), 'b:', ... | ||
t, IntXY(t), 'g--') | t, IntXY(t), 'g--') | ||
| − | legend('\int x(t)', '\int y(t)', '\int x(t) y(t)', | + | legend('\int x(t)', '\int y(t)', '\int x(t) y(t)', 'location','best') |
xlabel('t') | xlabel('t') | ||
gzoom | gzoom | ||
| Line 46: | Line 45: | ||
figure(1); print -dpng SignalPlot | figure(1); print -dpng SignalPlot | ||
figure(2); print -dpng IntegralPlot</source> | figure(2); print -dpng IntegralPlot</source> | ||
| + | |||
=== xMaple === | === xMaple === | ||
Note - for the xMaple code, if you copy and paste it, all the code will go in one execution group (thus the ; at the end of each line). I haven't figured out the smart way to put things in multiple lines... | Note - for the xMaple code, if you copy and paste it, all the code will go in one execution group (thus the ; at the end of each line). I haven't figured out the smart way to put things in multiple lines... | ||
Revision as of 22:34, 19 January 2017
The following is a demonstration of how to perform similar tasks in Maple and MATLAB. Specifically, this example shows how to define the unit step and ramp functions, use them to define accumulated signals, create functions to calculate the integrals of those signals, and plot both the signals and their integrals. The comments are meant to show the different sections of each piece of code. The resulting figures are connected with each particular program.
MATLAB
Code
% MATLAB and Maple Demo
% M. R. Gustafson II
%% Initialize
clear
%% Define step and ramp functions
ustep = @(in) (1.0).*(in>=0);
uramp = @(in) (in).*(in>=0);
%% Define x and y using accumulation
X = @(t) (-1)*uramp(t+1)+ustep(t)+(2)*uramp(t)+(-1)*uramp(t-1)+(-1)*uramp(t-2)+(1)*uramp(t-3);
Y = @(t) ustep(t+2)+(-2)*ustep(t+1)+uramp(t)+(-1)*uramp(t-1)+ustep(t-1)-ustep(t-2);
%% Plot signals
t = linspace(-4, 4, 1e4);
figure(1); clf
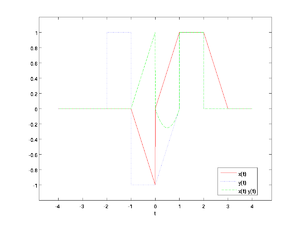
plot(t, X(t), 'r-', ...
t, Y(t), 'b:', ...
t, X(t).*Y(t), 'g--')
legend('x(t)', 'y(t)', 'x(t) y(t)', 'location','best')
xlabel('t')
gzoom
%% Calculate integrals
IntX = @(t) cumtrapz(t, X(t));
IntY = @(t) cumtrapz(t, Y(t));
IntXY = @(t) cumtrapz(t, X(t).*Y(t));
%% Plot integrals
figure(2); clf
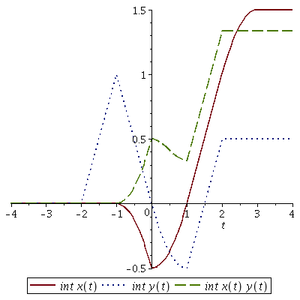
plot(t, IntX(t), 'r-', ...
t, IntY(t), 'b:', ...
t, IntXY(t), 'g--')
legend('\int x(t)', '\int y(t)', '\int x(t) y(t)', 'location','best')
xlabel('t')
gzoom
%% Save plots (not in Maple)
figure(1); print -dpng SignalPlot
figure(2); print -dpng IntegralPlot
xMaple
Note - for the xMaple code, if you copy and paste it, all the code will go in one execution group (thus the ; at the end of each line). I haven't figured out the smart way to put things in multiple lines...
# Maple and MATLAB Demo
# M. R. Gustafson II
# Fall 2013
# Initialize
restart;
# Define step and ramp functions
U := t-> Heaviside(t);
R := t-> t*U(t);
# Define x and y using accumulation
X := t-> -R(t+1)+U(t)+2*R(t)-R(t-1)-R(t-2)+R(t-3);
Y := t-> U(t+2)-2*U(t+1)+R(t)-R(t-1)+U(t-1)-U(t-2);
# Plot signals
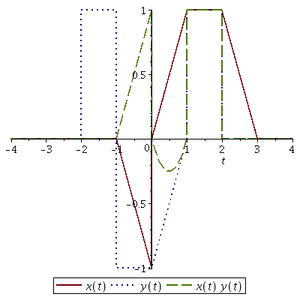
plot([X(t), Y(t), X(t)*Y(t)], t = -4 .. 4, linestyle = [1, 2, 3], legend = ['x(t)', 'y(t)', 'x(t)*y(t)']);
# Calculate integrals
IntX := t-> int(X(tau), tau = -infinity .. t);
IntY := t-> int(Y(tau), tau = -infinity .. t);
IntXY := t-> int(X(tau)*Y(tau), tau = -infinity .. t);
# Plot integrals
plot([IntX(t), IntY(t), IntXY(t)], t = -4 .. 4, linestyle = [1, 2, 3], legend = ['int*x(t)', 'int*y(t)', 'int*x(t)*y(t)']);