Difference between revisions of "MATLAB:Ordinary Differential Equations/Examples"
| Line 28: | Line 28: | ||
initial value of <math>y</math> is 6, and the rate of change is 1.2: | initial value of <math>y</math> is 6, and the rate of change is 1.2: | ||
<source lang="matlab"> | <source lang="matlab"> | ||
| − | clear; format short e | + | % Initialize workspace and graph |
| + | clear; format short e; figure(1); clf | ||
% Set name of file containing derivatives | % Set name of file containing derivatives | ||
| Line 82: | Line 83: | ||
[2 -6 3]: | [2 -6 3]: | ||
<source lang="matlab"> | <source lang="matlab"> | ||
| + | % Initialize workspace and graph | ||
| + | clear; format short e; figure(1); clf | ||
| + | |||
% Set name of file containing derivatives | % Set name of file containing derivatives | ||
DiffFileName = 'TimeDiff'; | DiffFileName = 'TimeDiff'; | ||
| Line 133: | Line 137: | ||
and a constant of proportionality of 1.02: | and a constant of proportionality of 1.02: | ||
<source lang="matlab"> | <source lang="matlab"> | ||
| + | % Initialize workspace and graph | ||
| + | clear; format short e; figure(1); clf | ||
| + | |||
% Set name of file containing derivatives | % Set name of file containing derivatives | ||
DiffFileName = 'PopDiff'; | DiffFileName = 'PopDiff'; | ||
Revision as of 19:53, 25 November 2009
The following examples show different ways of setting up and solving initial value problems in MATLAB. It is part of the page on Ordinary Differential Equations in MATLAB.
Contents
Examples
Note - each example began with the Templates provided at this web site. Some comments have been removed from the templates to conserve space while some comments may have been added to provide a clearer explanation of the process for a particular example.
Constant Rate of Change
If the dependent variable has a constant rate of change:
where \(k\) is some constant, you can provide the differential equation
with a function called ConstDiff.m that contains the code:
function dydt = ConstDiff(t, y, k)
% Differential equation for constant growth
% t is time
% y is the state vector
% k contains any required constants
% dydt must be a column vector
dydt = k(1); % or just k since there is only one
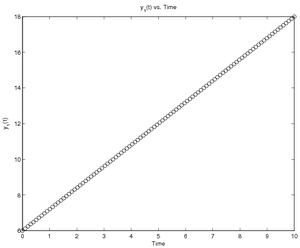
You could calculate answers using this model with the following code
called RunConstDiff.m,
which assumes there are 100 evenly spaced times between 0 and 10, the
initial value of \(y\) is 6, and the rate of change is 1.2:
% Initialize workspace and graph
clear; format short e; figure(1); clf
% Set name of file containing derivatives
DiffFileName = 'ConstDiff';
% Set up time span, initial value(s), and constant(s)
% Note: Variables should be in columns
tspan = linspace(0, 10);
yinit = 6;
k = 1.2;
% Determine if states should be plotted
PlotStates = 1;
%% Under the hood
% Use ODE function of choice to get output times and states
DE = eval(sprintf('@(t, y, k) %s(t,y,k)', DiffFileName))
[tout, yout] = ode45(@(t,y) DE(t,y,k), tspan, yinit);
% Plot results
if PlotStates
figure(1); clf
StatePlotter(tout, yout)
end
Time-dependent Rate of Change
If the dependent variable's rate of change is some function of time, this can be easily written using MATLAB. For example, if the differential equation is some quadratic function given as:
then the function providing the values of the derivative may be
written in a file called TimeDiff.m
function dydt = TimeDiff(t, y, k)
% Differential equation for time-based polynomial derivative
% t is time
% y is the state vector
% k contains any required constants
% dydt must be a column vector
dydt = polyval(k, t);
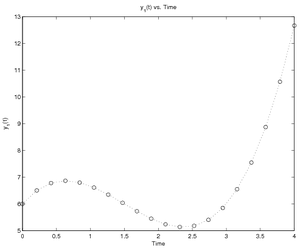
You could calculate answers using this model with the following code
called RunTimeDiff.m,
which assumes there are 20 evenly spaced times between 0 and 4, the
initial value of \(y\) is 6, and the polynomial is defined by the vector
[2 -6 3]:
% Initialize workspace and graph
clear; format short e; figure(1); clf
% Set name of file containing derivatives
DiffFileName = 'TimeDiff';
% Set up time span, initial value(s), and constant(s)
% Note: Variables should be in columns
tspan = linspace(0, 4, 20);
yinit = 6;
k = [2 -6 3];
% Determine if states should be plotted
PlotStates = 1;
%% Under the hood
% Use ODE function of choice to get output times and states
DE = eval(sprintf('@(t, y, k) %s(t,y,k)', DiffFileName))
[tout, yout] = ode45(@(t,y) DE(t,y,k), tspan, yinit);
% Plot results
if PlotStates
StatePlotter(tout, yout)
end
Population Growth
For population growth, the rate of change of population is dependent upon the number of people as well as some constant of proportionality:
where \(k\) is again some constant.
In that case, the function may be written in a file called PopDiff.m as follows:
function dydt = PopDiff(t, y, k)
% Differential equation for population growth
% t is time
% y is the state vector
% k contains any required constants
% dydt must be a column vector
dydt = k(1)*y(1); % or just k*y since both are 1x1
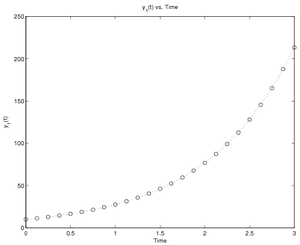
The following code, RunPopDiff.m, will calculate the population for
a span of 3 seconds with 25
points for the population model above with an initial population of 10
and a constant of proportionality of 1.02:
% Initialize workspace and graph
clear; format short e; figure(1); clf
% Set name of file containing derivatives
DiffFileName = 'PopDiff';
% Set up time span, initial value(s), and constant(s)
% Note: Variables should be in columns
tspan = linspace(0, 3, 25);
yinit = 10;
k = 1.02;
% Determine if states should be plotted
PlotStates = 1;
%% Under the hood
% Use ODE function of choice to get output times and states
DE = eval(sprintf('@(t, y, k) %s(t,y,k)', DiffFileName))
[tout, yout] = ode45(@(t,y) DE(t,y,k), tspan, yinit);
% Plot results
if PlotStates
StatePlotter(tout, yout)
end
Questions
Post your questions by editing the discussion page of this article. Edit the page, then scroll to the bottom and add a question by putting in the characters *{{Q}}, followed by your question and finally your signature (with four tildes, i.e. ~~~~). Using the {{Q}} will automatically put the page in the category of pages with questions - other editors hoping to help out can then go to that category page to see where the questions are. See the page for Template:Q for details and examples.