Difference between revisions of "ECE 280/Examples/Convolution"
Jump to navigation
Jump to search
\(
\begin{align}
x(t)&=2u(t)-u(t-1)-u(t-3)\\
h(t)&=e^{-t}u(t)\\
y(t)&=x(t)*h(t)=\int_{-\infty}^{\infty}x(\tau)h(t-\tau)d\tau=\int_{-\infty}^{\infty}x(t-\tau)h(\tau)d\tau
\end{align}
\)
\(
\begin{align}
y(t)&=\int_{-\infty}^{\infty}x(\tau)h(t-\tau)d\tau\\
y(t)&=\int_{-\infty}^{\infty}\left(2u(\tau)-u(\tau-1)-u(\tau-3)\right)\left(e^{-(t-\tau)}u(t-\tau)\right)d\tau
\end{align}
\)
\(
\begin{align}
y(t)&=\int_{-\infty}^{\infty}2e^{-(t-\tau)}u(\tau)u(t-\tau)d\tau\dots\\
~&~-\int_{-\infty}^{\infty}e^{-(t-\tau)}u(\tau-1)u(t-\tau)d\tau\dots\\
~&~-\int_{-\infty}^{\infty}e^{-(t-\tau)}u(\tau-3)u(t-\tau)d\tau\\
\end{align}
\)
\(
\int_{-\infty}^{\infty}{\color{Brown}2e^{-(t-\tau)}}{\color{Red}u(\tau)}{\color{Blue}u(t-\tau)}d\tau
\)
\(
\begin{align}
{\color{Red}0}&{\color{Red}<\tau} & {\color{Blue}\tau}&{\color{Blue}<t}
\end{align}
\)
\(
\begin{align}
{\color{Purple}0}&{\color{Purple}<t}
\end{align}
\)
\(
\begin{align}
\int_{-\infty}^{\infty}{\color{Brown}2e^{-(t-\tau)}}{\color{Red}u(\tau)}{\color{Blue}u(t-\tau)}d\tau &=
{\color{Purple}u(t)}\int_{{\color{Red}0}}^{{\color{Blue}t}}{\color{Brown}2e^{-(t-\tau)}}d\tau\\
{\color{Purple}u(t)}\int_{{\color{Red}0}}^{{\color{Blue}t}}{\color{Brown}2e^{-(t-\tau)}}d\tau&=
u(t)\left[2e^{-(t-\tau)} \right]_0^{t}=\left(2-2e^{-t}\right)u(t)
\end{align}
\)
\(
\begin{align}
\int_{-\infty}^{\infty}{\color{Brown}-e^{-(t-\tau)}}{\color{Red}u(\tau-1)}{\color{Blue}u(t-\tau)}d\tau &=
{\color{Purple}u(t-1)}\int_{{\color{Red}1}}^{{\color{Blue}t}}{\color{Brown}-e^{-(t-\tau)}}d\tau\\
{\color{Purple}u(t-1)}\int_{{\color{Red}1}}^{{\color{Blue}t}}{\color{Brown}-e^{-(t-\tau)}}d\tau&=
-u(t-1)\left[e^{-(t-\tau)} \right]_1^{t}=-\left(1-1e^{-(t-1)}\right)u(t-1)
\end{align}
\)
\(
\begin{align}
\int_{-\infty}^{\infty}{\color{Brown}-e^{-(t-\tau)}}{\color{Red}u(\tau-3)}{\color{Blue}u(t-\tau)}d\tau &=
{\color{Purple}u(t-3)}\int_{{\color{Red}3}}^{{\color{Blue}t}}{\color{Brown}-e^{-(t-\tau)}}d\tau\\
{\color{Purple}u(t-3)}\int_{{\color{Red}3}}^{{\color{Blue}t}}{\color{Brown}-e^{-(t-\tau)}}d\tau&=
-u(t-3)\left[e^{-(t-\tau)} \right]_3^{t}=-\left(1-1e^{-(t-3)}\right)u(t-3)
\end{align}
\)
\(
\begin{align}
y(t)=x(t)*h(t)=\left(2-2e^{-t}\right)u(t)-\left(1-1e^{-(t-1)}\right)u(t-1)-\left(1-1e^{-(t-3)}\right)u(t-3)
\end{align}
\)
\(
\begin{align}
y(t)&=\begin{cases} {\color{Black}0} & {\color{Black}t<0} \\
2-2e^{-t} & {\color{Black}0<t<1}\\
1 - 2e^{-t}+ e^{-(t-1)} & {\color{Black}1<t<3}\\
-2e^{-t} + e^{-(t-1)} + e^{-(t-3)} & {\color{Black}t>3}
\end{cases}
\end{align}
\)
\(
\begin{align}
x(t)&=\color{Brown}{2u(t)-u(t-1)-u(t-3)}\\
h(t)&=\color{Blue}{e^{-t}u(t)}\\
x(t)*h(t)&=\color{Brown}{2u(t)}*\color{Blue}{e^{-t}u(t)}\color{Brown}{-u(t-1)}*\color{Blue}{e^{-t}u(t)}\color{Brown}{-u(t-3)}*\color{Blue}{e^{-t}u(t)}
\end{align}
\)
\(
\begin{align}
x(t)*h(t)&=\color{Orange}{2}\color{Blue}{e^{-t}u(t)}*\color{Red}{u(t)}\color{Orange}{-}\color{Blue}{e^{-t}u(t)}*\color{Red}{u(t)}\color{Orange}{*\delta(t-1)}\color{Orange}{-}\color{Blue}{e^{-t}u(t)}*\color{Red}{u(t)}\color{Orange}{*\delta(t-3)}
\end{align}
\)
\(
\begin{align}
\color{Blue}{e^{-t}u(t)}*\color{Red}{u(t)}
\end{align}
\)
\(
\begin{align}
\color{Red}{\int_{-\infty}^{t}}\color{Blue}{e^{-\tau}u(\tau)}d\tau=u(t)\left[-e^{-\tau}\right]_0^t=\color{Fuchsia}{(1-e^{-t})u(t)}
\end{align}
\)
\(
\begin{align}
x(t)*h(t)&=\color{Orange}{2}\color{Fuchsia}{(1-e^{-t})u(t)}\color{Orange}{-}\color{Fuchsia}{(1-e^{-t})u(t)}\color{Orange}{*\delta(t-1)}\color{Orange}{-}\color{Fuchsia}{(1-e^{-t})u(t)}\color{Orange}{*\delta(t-3)}
\end{align}
\)
\(
\begin{align}
x(t)*h(t)&=2(1-e^{-t})u(t)-(1-e^{-(t-1)})u(t-1)-(1-e^{-(t-3)})u(t-3)
\end{align}
\)
\(
\begin{align}
x(t)&={\color{Black}2u(t)-u(t-1)-u(t-3)}\\
h(t)&={\color{Black}e^{-t}u(t)}\\
x(t)*h(t)&={\color{Black}2u(t)}*{\color{Black}e^{-t}u(t)}{\color{Black}-u(t-1)}*{\color{Black}e^{-t}u(t)}{\color{Black}-u(t-3)}*{\color{Black}e^{-t}u(t)}
\end{align}
\)
\(
\begin{align}
x(t)*h(t)&={\color{Black}2}{\color{Black}e^{-t}u(t)}*{\color{Black}u(t)}{\color{Black}-}{\color{Black}e^{-t}u(t)}*{\color{Black}u(t)}{\color{Black}*\delta(t-1)}{\color{Black}-}{\color{Black}e^{-t}u(t)}*{\color{Black}u(t)}{\color{Black}*\delta(t-3)}
\end{align}
\)
\(
\begin{align}
{\color{Black}e^{-t}u(t)}*{\color{Black}u(t)}
\end{align}
\)
\(
\begin{align}
{\color{Black}\int_{-\infty}^{t}}{\color{Black}e^{-\tau}u(\tau)}d\tau=u(t)\left[-e^{-\tau}\right]_0^t={\color{Black}(1-e^{-t})u(t)}
\end{align}
\)
\(
\begin{align}
x(t)*h(t)&={\color{Black}2}{\color{Black}(1-e^{-t})u(t)}{\color{Black}-}{\color{Black}(1-e^{-t})u(t)}{\color{Black}*\delta(t-1)}{\color{Black}-}{\color{Black}(1-e^{-t})u(t)}{\color{Black}*\delta(t-3)}
\end{align}
\)
\(
\begin{align}
x(t)*h(t)&=2(1-e^{-t})u(t)-(1-e^{-(t-1)})u(t-1)-(1-e^{-(t-3)})u(t-3)
\end{align}
\)
\(
\begin{align}
x(t)&= \begin{cases} 0 & t<0 \\ 2 & 0<t<1 \\ 1 & 1<t<3 \\ 0 & t>3\end{cases} &
h(t)&= \begin{cases} 0 & t<0 \\ e^{-t} & t>0\end{cases} &
\end{align}
\)
\(
\begin{align}
y(t)&=x(t)*h(t)=\int_{-\infty}^{\infty}x(\tau)h(t-\tau)d\tau
\end{align}
\)
\(
\begin{align}
x(\tau)&= \begin{cases} 0 & \tau<0 \\ 2 & 0<\tau<1 \\ 1 & 1<\tau<3 \\ 0 & t>3\end{cases} &
h(t-\tau)&= \begin{cases} e^{-(t-\tau)} & \tau<t \\ 0 & \tau>t\end{cases}
\end{align}
\)
\(
\begin{align}
y(t)&=\begin{cases} {\color{Black}0} & {\color{Black}t<0} \end{cases}
\end{align}
\)
\(
\begin{align}
y(t)&=\begin{cases} {\color{Black}0} & {\color{Black}t<0} \\
{\color{Black}\int_{{\color{Red}0}}^{{\color{Blue}t}}{\color{Red}2}{\color{Blue}e^{-(t-\tau)}}~d\tau} & {\color{Black}0<t<1}
\end{cases}
\end{align}
\)
\(
\begin{align}
y(t)&=\begin{cases} {\color{Black}0} & {\color{Black}t<0} \\
{\color{Black}\int_{{\color{Red}0}}^{{\color{Blue}t}}{\color{Red}2}{\color{Blue}e^{-(t-\tau)}}~d\tau} & {\color{Black}0<t<1}\\
{\color{Black}\int_{{\color{Red}0}}^{{\color{Red}1}}{\color{Red}2}{\color{Blue}e^{-(t-\tau)}}~d\tau} +
{\color{Black}\int_{{\color{Red}1}}^{{\color{Blue}t}}{\color{Red}1}{\color{Blue}e^{-(t-\tau)}}~d\tau} & {\color{Black}1<t<3}
\end{cases}
\end{align}
\)
\(
\begin{align}
y(t)&=\begin{cases} {\color{Black}0} & {\color{Black}t<0} \\
{\color{Black}\int_{{\color{Red}0}}^{{\color{Blue}t}}{\color{Red}2}{\color{Blue}e^{-(t-\tau)}}~d\tau} & {\color{Black}0<t<1}\\
{\color{Black}\int_{{\color{Red}0}}^{{\color{Red}1}}{\color{Red}2}{\color{Blue}e^{-(t-\tau)}}~d\tau} +
{\color{Black}\int_{{\color{Red}1}}^{{\color{Blue}t}}{\color{Red}1}{\color{Blue}e^{-(t-\tau)}}~d\tau} & {\color{Black}1<t<3}\\
{\color{Black}\int_{{\color{Red}0}}^{{\color{Red}1}}{\color{Red}2}{\color{Blue}e^{-(t-\tau)}}~d\tau} +
{\color{Black}\int_{{\color{Red}1}}^{{\color{Red}3}}{\color{Red}1}{\color{Blue}e^{-(t-\tau)}}~d\tau} & {\color{Black}t>3}
\end{cases}
\end{align}
\)
\(
\begin{align}
y(t)&=\begin{cases} {\color{Black}0} & {\color{Black}t<0} \\
2-2e^{-t} & {\color{Black}0<t<1}\\
(2e^{-(t-1)}-2e^{-t})+(1-e^{-(t-1)}) & {\color{Black}1<t<3}\\
(2e^{-(t-1)}-2e^{-t}) + (e^{-(t-3)}-e^{-(t-1)})& {\color{Black}t>3}
\end{cases}
\end{align}
\)
\(
\begin{align}
y(t)&=\begin{cases} {\color{Black}0} & {\color{Black}t<0} \\
2-2e^{-t} & {\color{Black}0<t<1}\\
1 - 2e^{-t}+ e^{-(t-1)} & {\color{Black}1<t<3}\\
-2e^{-t} + e^{-(t-1)} + e^{-(t-3)} & {\color{Black}t>3}
\end{cases}
\end{align}
\)
\(
\begin{align}
x(t)&= \begin{cases} 0 & t<0 \\ 2 & 0<t<1 \\ 1 & 1<t<3 \\ 0 & t>3\end{cases} &
h(t)&= \begin{cases} 0 & t<0 \\ e^{-t} & t>0\end{cases} &
\end{align}
\)
\(
\begin{align}
y(t)&=x(t)*h(t)=\int_{-\infty}^{\infty}x(t-\tau)h(t)d\tau
\end{align}
\)
\(
\begin{align}
x(t-\tau)&= \begin{cases} 0 & \tau<t-3 \\ 1 & t-3<\tau<t-1 \\ 2 & t-1<\tau<0 \\ 0 & \tau>3\end{cases} &
h(\tau)&= \begin{cases} 0 & \tau<0 \\ e^{-\tau} & \tau>0\end{cases}
\end{align}
\)
\(
\begin{align}
y(t)&=\begin{cases} {\color{Black}0} & {\color{Black}t<0} \end{cases}
\end{align}
\)
\(
\begin{align}
y(t)&=\begin{cases} {\color{Black}0} & {\color{Black}t<0} \\
{\color{Black}\int_{{\color{Blue}0}}^{{\color{Red}t}}{\color{Red}2}{\color{Blue}e^{-\tau}}~d\tau} & {\color{Black}0<t<1}
\end{cases}
\end{align}
\)
\(
\begin{align}
y(t)&=\begin{cases} {\color{Black}0} & {\color{Black}t<0} \\
{\color{Black}\int_{{\color{Blue}0}}^{{\color{Red}t}}{\color{Red}2}{\color{Blue}e^{-\tau}}~d\tau} & {\color{Black}0<t<1} \\
{\color{Black}\int_{{\color{Blue}0}}^{{\color{Red}t-1}}{\color{Red}1}{\color{Blue}e^{-\tau}}~d\tau} +
{\color{Black}\int_{{\color{Red}t-1}}^{{\color{Red}t}}{\color{Red}2}{\color{Blue}e^{-\tau}}~d\tau} & {\color{Black}1<t<3}
\end{cases}
\end{align}
\)
\(
\begin{align}
y(t)&=\begin{cases} {\color{Black}0} & {\color{Black}t<0} \\
{\color{Black}\int_{{\color{Blue}0}}^{{\color{Red}t}}{\color{Red}2}{\color{Blue}e^{-\tau}}~d\tau} & {\color{Black}0<t<1} \\
{\color{Black}\int_{{\color{Blue}0}}^{{\color{Red}t-1}}{\color{Red}1}{\color{Blue}e^{-\tau}}~d\tau} +
{\color{Black}\int_{{\color{Red}t-1}}^{{\color{Red}t}}{\color{Red}2}{\color{Blue}e^{-\tau}}~d\tau} & {\color{Black}1<t<3}\\
{\color{Black}\int_{{\color{Red}t-3}}^{{\color{Red}t-1}}{\color{Red}1}{\color{Blue}e^{-\tau}}~d\tau} +
{\color{Black}\int_{{\color{Red}t-1}}^{{\color{Red}t}}{\color{Red}2}{\color{Blue}e^{-\tau}}~d\tau} & {\color{Black}t>3}
\end{cases}
\end{align}
\)
| (16 intermediate revisions by the same user not shown) | |||
| Line 82: | Line 82: | ||
\begin{align} | \begin{align} | ||
y(t)=x(t)*h(t)=\left(2-2e^{-t}\right)u(t)-\left(1-1e^{-(t-1)}\right)u(t-1)-\left(1-1e^{-(t-3)}\right)u(t-3) | y(t)=x(t)*h(t)=\left(2-2e^{-t}\right)u(t)-\left(1-1e^{-(t-1)}\right)u(t-1)-\left(1-1e^{-(t-3)}\right)u(t-3) | ||
| + | \end{align} | ||
| + | </math></center> | ||
| + | Written piecewise, this equation would be: | ||
| + | <center><math> | ||
| + | \begin{align} | ||
| + | y(t)&=\begin{cases} {\color{Black}0} & {\color{Black}t<0} \\ | ||
| + | 2-2e^{-t} & {\color{Black}0<t<1}\\ | ||
| + | 1 - 2e^{-t}+ e^{-(t-1)} & {\color{Black}1<t<3}\\ | ||
| + | -2e^{-t} + e^{-(t-1)} + e^{-(t-3)} & {\color{Black}t>3} | ||
| + | \end{cases} | ||
\end{align} | \end{align} | ||
</math></center> | </math></center> | ||
== Shortcuts == | == Shortcuts == | ||
| + | <div class="toccolours mw-collapsible" style="width:800px"> | ||
| + | Full color version: | ||
| + | <div class="mw-collapsible-content"> | ||
To use the shortcuts, first distribute the various components of the convolution: | To use the shortcuts, first distribute the various components of the convolution: | ||
<center><math> | <center><math> | ||
\begin{align} | \begin{align} | ||
| − | x(t)&=2u(t)-u(t-1)-u(t-3)\\ | + | x(t)&=\color{Brown}{2u(t)-u(t-1)-u(t-3)}\\ |
| − | h(t)&=e^{-t}u(t)\\ | + | h(t)&=\color{Blue}{e^{-t}u(t)}\\ |
| − | x(t)*h(t)&=2u(t)*e^{-t}u(t)-u(t-1)*e^{-t}u(t)-u(t-3)*e^{-t}u(t) | + | x(t)*h(t)&=\color{Brown}{2u(t)}*\color{Blue}{e^{-t}u(t)}\color{Brown}{-u(t-1)}*\color{Blue}{e^{-t}u(t)}\color{Brown}{-u(t-3)}*\color{Blue}{e^{-t}u(t)} |
\end{align} | \end{align} | ||
</math></center> | </math></center> | ||
| Line 97: | Line 110: | ||
<center><math> | <center><math> | ||
\begin{align} | \begin{align} | ||
| − | x(t)*h(t)&= | + | x(t)*h(t)&=\color{Orange}{2}\color{Blue}{e^{-t}u(t)}*\color{Red}{u(t)}\color{Orange}{-}\color{Blue}{e^{-t}u(t)}*\color{Red}{u(t)}\color{Orange}{*\delta(t-1)}\color{Orange}{-}\color{Blue}{e^{-t}u(t)}*\color{Red}{u(t)}\color{Orange}{*\delta(t-3)} |
\end{align} | \end{align} | ||
</math></center> | </math></center> | ||
| Line 103: | Line 116: | ||
<center><math> | <center><math> | ||
\begin{align} | \begin{align} | ||
| − | e^{-t}u(t)*u(t) | + | \color{Blue}{e^{-t}u(t)}*\color{Red}{u(t)} |
\end{align} | \end{align} | ||
</math></center> | </math></center> | ||
| Line 109: | Line 122: | ||
<center><math> | <center><math> | ||
\begin{align} | \begin{align} | ||
| − | \int_{-\infty}^{t}e^{-\tau}u(\tau)d\tau=u(t)\left[-e^{-\tau}\right]_0^t=(1-e^{-t})u(t) | + | \color{Red}{\int_{-\infty}^{t}}\color{Blue}{e^{-\tau}u(\tau)}d\tau=u(t)\left[-e^{-\tau}\right]_0^t=\color{Fuchsia}{(1-e^{-t})u(t)} |
\end{align} | \end{align} | ||
</math></center> | </math></center> | ||
| Line 115: | Line 128: | ||
<center><math> | <center><math> | ||
\begin{align} | \begin{align} | ||
| − | x(t)*h(t)&=2(1-e^{-t})u(t)-(1-e^{-t})u(t)*\delta(t-1)-(1-e^{-t})u(t)*\delta(t-3) | + | x(t)*h(t)&=\color{Orange}{2}\color{Fuchsia}{(1-e^{-t})u(t)}\color{Orange}{-}\color{Fuchsia}{(1-e^{-t})u(t)}\color{Orange}{*\delta(t-1)}\color{Orange}{-}\color{Fuchsia}{(1-e^{-t})u(t)}\color{Orange}{*\delta(t-3)} |
\end{align} | \end{align} | ||
</math></center> | </math></center> | ||
| Line 124: | Line 137: | ||
\end{align} | \end{align} | ||
</math></center> | </math></center> | ||
| + | </div> | ||
| + | </div> | ||
| + | |||
| + | <div class="toccolours mw-collapsible mw-collapsed" style="width:800px"> | ||
| + | Black and white only: | ||
| + | <div class="mw-collapsible-content"> | ||
| + | To use the shortcuts, first distribute the various components of the convolution: | ||
| + | <center><math> | ||
| + | \begin{align} | ||
| + | x(t)&={\color{Black}2u(t)-u(t-1)-u(t-3)}\\ | ||
| + | h(t)&={\color{Black}e^{-t}u(t)}\\ | ||
| + | x(t)*h(t)&={\color{Black}2u(t)}*{\color{Black}e^{-t}u(t)}{\color{Black}-u(t-1)}*{\color{Black}e^{-t}u(t)}{\color{Black}-u(t-3)}*{\color{Black}e^{-t}u(t)} | ||
| + | \end{align} | ||
| + | </math></center> | ||
| + | These can be rearranged, pulling out any shifts, as: | ||
| + | <center><math> | ||
| + | \begin{align} | ||
| + | x(t)*h(t)&={\color{Black}2}{\color{Black}e^{-t}u(t)}*{\color{Black}u(t)}{\color{Black}-}{\color{Black}e^{-t}u(t)}*{\color{Black}u(t)}{\color{Black}*\delta(t-1)}{\color{Black}-}{\color{Black}e^{-t}u(t)}*{\color{Black}u(t)}{\color{Black}*\delta(t-3)} | ||
| + | \end{align} | ||
| + | </math></center> | ||
| + | Note that each component now has a convolution of | ||
| + | <center><math> | ||
| + | \begin{align} | ||
| + | {\color{Black}e^{-t}u(t)}*{\color{Black}u(t)} | ||
| + | \end{align} | ||
| + | </math></center> | ||
| + | in it. Convolution with a step generates an integral, and integrating the right-sided exponential yields: | ||
| + | <center><math> | ||
| + | \begin{align} | ||
| + | {\color{Black}\int_{-\infty}^{t}}{\color{Black}e^{-\tau}u(\tau)}d\tau=u(t)\left[-e^{-\tau}\right]_0^t={\color{Black}(1-e^{-t})u(t)} | ||
| + | \end{align} | ||
| + | </math></center> | ||
| + | which means the rearranged functions can be re-written as: | ||
| + | <center><math> | ||
| + | \begin{align} | ||
| + | x(t)*h(t)&={\color{Black}2}{\color{Black}(1-e^{-t})u(t)}{\color{Black}-}{\color{Black}(1-e^{-t})u(t)}{\color{Black}*\delta(t-1)}{\color{Black}-}{\color{Black}(1-e^{-t})u(t)}{\color{Black}*\delta(t-3)} | ||
| + | \end{align} | ||
| + | </math></center> | ||
| + | Now the shifts can be applied to give: | ||
| + | <center><math> | ||
| + | \begin{align} | ||
| + | x(t)*h(t)&=2(1-e^{-t})u(t)-(1-e^{-(t-1)})u(t-1)-(1-e^{-(t-3)})u(t-3) | ||
| + | \end{align} | ||
| + | </math></center> | ||
| + | </div> | ||
| + | </div> | ||
| + | |||
| + | == Geometrically Flipping/Shifting <math>h</math> == | ||
| + | The geometric method involves determining the piecewise regions in <math>\tau</math> where the different functions overlap as a function of <math>t</math>. With the current example, the only change <math>h(t)</math> makes is at <math>t=0</math>, while <math>x(t)</math> has four different parts. The piecewise definitions of the two functions can be written as: | ||
| + | <center><math> | ||
| + | \begin{align} | ||
| + | x(t)&= \begin{cases} 0 & t<0 \\ 2 & 0<t<1 \\ 1 & 1<t<3 \\ 0 & t>3\end{cases} & | ||
| + | h(t)&= \begin{cases} 0 & t<0 \\ e^{-t} & t>0\end{cases} & | ||
| + | \end{align} | ||
| + | </math></center> | ||
| + | In the convolution integral | ||
| + | <center><math> | ||
| + | \begin{align} | ||
| + | y(t)&=x(t)*h(t)=\int_{-\infty}^{\infty}x(\tau)h(t-\tau)d\tau | ||
| + | \end{align} | ||
| + | </math></center> | ||
| + | the piecewise definitions of the signals change to functions of <math>\tau</math>: | ||
| + | <center><math> | ||
| + | \begin{align} | ||
| + | x(\tau)&= \begin{cases} 0 & \tau<0 \\ 2 & 0<\tau<1 \\ 1 & 1<\tau<3 \\ 0 & t>3\end{cases} & | ||
| + | h(t-\tau)&= \begin{cases} e^{-(t-\tau)} & \tau<t \\ 0 & \tau>t\end{cases} | ||
| + | \end{align} | ||
| + | </math></center> | ||
| + | As <math>t</math> changes, <math>x(\tau)</math> does not move but <math>h(t-\tau)</math> does, resulting in different components of the two functions overlapping at different times. The following four subsections will show what happens as <math>t</math> increases. | ||
| + | === t<0 === | ||
| + | [[File:ConvDemo01p1H.png|200px|thumb|right|Before overlap]] | ||
| + | The "leading edge" of <math>h(t-\tau)</math> is at <math>\tau=t</math>; until <math>t>0</math>, there will be no overlap with <math>x(\tau)</math> and thus the convolution integral will be 0: | ||
| + | <center><math> | ||
| + | \begin{align} | ||
| + | y(t)&=\begin{cases} {\color{Black}0} & {\color{Black}t<0} \end{cases} | ||
| + | \end{align} | ||
| + | </math></center> | ||
| + | <br clear=all> | ||
| + | === 0<t<1 === | ||
| + | [[File:ConvDemo01p2H.png|200px|thumb|right|First overlap]] | ||
| + | Once <math>t>0</math>, the segment of <math>h</math> that is nonzero passes into the region of <math>x</math> that is equal to the constant 2. This will remain the situation until <math>h</math>'s transition into the region where <math>x</math> is 1. During this phase, the integrand will be the product of the exponential from <math>h</math> and the 2 from <math>x</math>: | ||
| + | <center><math> | ||
| + | \begin{align} | ||
| + | y(t)&=\begin{cases} {\color{Black}0} & {\color{Black}t<0} \\ | ||
| + | {\color{Black}\int_{{\color{Red}0}}^{{\color{Blue}t}}{\color{Red}2}{\color{Blue}e^{-(t-\tau)}}~d\tau} & {\color{Black}0<t<1} | ||
| + | \end{cases} | ||
| + | \end{align} | ||
| + | </math></center> | ||
| + | <br clear=all> | ||
| + | === 1<t<3 === | ||
| + | [[File:ConvDemo01p3H.png|200px|thumb|right|Second overlap]] | ||
| + | After <math>t>1</math> but before <math>t>3</math>, there are two different regions of overlap: the region where <math>x</math> is 2 now overlaps for <math>0<\tau<1</math> while the region where <math>x</math> is 1 overlaps where <math>1<\tau<t</math>. | ||
| + | That yields: | ||
| + | <center><math> | ||
| + | \begin{align} | ||
| + | y(t)&=\begin{cases} {\color{Black}0} & {\color{Black}t<0} \\ | ||
| + | {\color{Black}\int_{{\color{Red}0}}^{{\color{Blue}t}}{\color{Red}2}{\color{Blue}e^{-(t-\tau)}}~d\tau} & {\color{Black}0<t<1}\\ | ||
| + | {\color{Black}\int_{{\color{Red}0}}^{{\color{Red}1}}{\color{Red}2}{\color{Blue}e^{-(t-\tau)}}~d\tau} + | ||
| + | {\color{Black}\int_{{\color{Red}1}}^{{\color{Blue}t}}{\color{Red}1}{\color{Blue}e^{-(t-\tau)}}~d\tau} & {\color{Black}1<t<3} | ||
| + | \end{cases} | ||
| + | \end{align} | ||
| + | </math></center> | ||
| + | <br clear=all> | ||
| + | === t>3 === | ||
| + | [[File:ConvDemo01p4H.png|200px|thumb|right|Final overlap]] | ||
| + | Finally, once <math>t>3</math>, the leading edge of the flipped <math>h</math> has passed the edge of <math>x</math> and the limits of integration are thus purely dependent on the piecewise boundaries of <math>x</math> alone: | ||
| + | <center><math> | ||
| + | \begin{align} | ||
| + | y(t)&=\begin{cases} {\color{Black}0} & {\color{Black}t<0} \\ | ||
| + | {\color{Black}\int_{{\color{Red}0}}^{{\color{Blue}t}}{\color{Red}2}{\color{Blue}e^{-(t-\tau)}}~d\tau} & {\color{Black}0<t<1}\\ | ||
| + | {\color{Black}\int_{{\color{Red}0}}^{{\color{Red}1}}{\color{Red}2}{\color{Blue}e^{-(t-\tau)}}~d\tau} + | ||
| + | {\color{Black}\int_{{\color{Red}1}}^{{\color{Blue}t}}{\color{Red}1}{\color{Blue}e^{-(t-\tau)}}~d\tau} & {\color{Black}1<t<3}\\ | ||
| + | {\color{Black}\int_{{\color{Red}0}}^{{\color{Red}1}}{\color{Red}2}{\color{Blue}e^{-(t-\tau)}}~d\tau} + | ||
| + | {\color{Black}\int_{{\color{Red}1}}^{{\color{Red}3}}{\color{Red}1}{\color{Blue}e^{-(t-\tau)}}~d\tau} & {\color{Black}t>3} | ||
| + | \end{cases} | ||
| + | \end{align} | ||
| + | </math></center> | ||
| + | === After Integration === | ||
| + | After calculating all those integrals, the answer would be: | ||
| + | <center><math> | ||
| + | \begin{align} | ||
| + | y(t)&=\begin{cases} {\color{Black}0} & {\color{Black}t<0} \\ | ||
| + | 2-2e^{-t} & {\color{Black}0<t<1}\\ | ||
| + | (2e^{-(t-1)}-2e^{-t})+(1-e^{-(t-1)}) & {\color{Black}1<t<3}\\ | ||
| + | (2e^{-(t-1)}-2e^{-t}) + (e^{-(t-3)}-e^{-(t-1)})& {\color{Black}t>3} | ||
| + | \end{cases} | ||
| + | \end{align} | ||
| + | </math></center> | ||
| + | or, combined, | ||
| + | <center><math> | ||
| + | \begin{align} | ||
| + | y(t)&=\begin{cases} {\color{Black}0} & {\color{Black}t<0} \\ | ||
| + | 2-2e^{-t} & {\color{Black}0<t<1}\\ | ||
| + | 1 - 2e^{-t}+ e^{-(t-1)} & {\color{Black}1<t<3}\\ | ||
| + | -2e^{-t} + e^{-(t-1)} + e^{-(t-3)} & {\color{Black}t>3} | ||
| + | \end{cases} | ||
| + | \end{align} | ||
| + | </math></center> | ||
| + | |||
| + | <br clear=all> | ||
| + | |||
| + | == Geometrically Flipping/Shifting x == | ||
| + | The geometric method involves determining the piecewise regions in <math>\tau</math> where the different functions overlap as a function of <math>t</math>. With the current example, the only change $h(t)$ makes is at <math>t=0</math>, while <math>x(t)</math> has four different parts. The piecewise definitions of the two functions can be written as: | ||
| + | <center><math> | ||
| + | \begin{align} | ||
| + | x(t)&= \begin{cases} 0 & t<0 \\ 2 & 0<t<1 \\ 1 & 1<t<3 \\ 0 & t>3\end{cases} & | ||
| + | h(t)&= \begin{cases} 0 & t<0 \\ e^{-t} & t>0\end{cases} & | ||
| + | \end{align} | ||
| + | </math></center> | ||
| + | In the convolution integral | ||
| + | <center><math> | ||
| + | \begin{align} | ||
| + | y(t)&=x(t)*h(t)=\int_{-\infty}^{\infty}x(t-\tau)h(t)d\tau | ||
| + | \end{align} | ||
| + | </math></center> | ||
| + | the piecewise definitions of the signals change to functions of <math>\tau</math>: | ||
| + | <center><math> | ||
| + | \begin{align} | ||
| + | x(t-\tau)&= \begin{cases} 0 & \tau<t-3 \\ 1 & t-3<\tau<t-1 \\ 2 & t-1<\tau<0 \\ 0 & \tau>3\end{cases} & | ||
| + | h(\tau)&= \begin{cases} 0 & \tau<0 \\ e^{-\tau} & \tau>0\end{cases} | ||
| + | \end{align} | ||
| + | </math></center> | ||
| + | As <math>t</math> changes, <math>h(\tau)</math> does not move but <math>x(t-\tau)</math> does, resulting in different components of the two functions overlapping at different times. The following four subsections will show what happens as <math>t</math> increases. | ||
| + | === t<0 === | ||
| + | [[File:ConvDemo01p1.png|200px|thumb|right|Before overlap]] | ||
| + | The "leading edge" of <math>x(t-\tau)</math> is at <math>\tau=t</math>; until <math>t>0</math>, there will be no overlap with <math>h(\tau)</math> and thus the convolution integral will be 0: | ||
| + | <center><math> | ||
| + | \begin{align} | ||
| + | y(t)&=\begin{cases} {\color{Black}0} & {\color{Black}t<0} \end{cases} | ||
| + | \end{align} | ||
| + | </math></center> | ||
| + | <br clear=all> | ||
| + | === 0<t<1 === | ||
| + | [[File:ConvDemo01p2.png|200px|thumb|right|First overlap]] | ||
| + | Once <math>t>0</math>, the segment of <math>x</math> that is equal to the constant 2 passes into the region of <math>h</math> that is non-zero. This will remain the situation until <math>x</math>'s transition to the constant 1 passes into that region. During this phase, the integrand will be the product of the exponential from <math>h</math> and the 2 from <math>x</math>: | ||
| + | <center><math> | ||
| + | \begin{align} | ||
| + | y(t)&=\begin{cases} {\color{Black}0} & {\color{Black}t<0} \\ | ||
| + | {\color{Black}\int_{{\color{Blue}0}}^{{\color{Red}t}}{\color{Red}2}{\color{Blue}e^{-\tau}}~d\tau} & {\color{Black}0<t<1} | ||
| + | \end{cases} | ||
| + | \end{align} | ||
| + | </math></center> | ||
| + | <br clear=all> | ||
| + | === 1<t<3 === | ||
| + | [[File:ConvDemo01p3.png|200px|thumb|right|Second overlap]] | ||
| + | After <math>t>1</math> but before <math>t>3</math>, there are two different regions of overlap: the region where <math>x</math> is 1 now overlaps for <math>0<\tau<t-1</math> while the region where <math>x</math> is 2 overlaps where <math>t-1<\tau<t-3</math>. | ||
| + | That yields: | ||
| + | <center><math> | ||
| + | \begin{align} | ||
| + | y(t)&=\begin{cases} {\color{Black}0} & {\color{Black}t<0} \\ | ||
| + | {\color{Black}\int_{{\color{Blue}0}}^{{\color{Red}t}}{\color{Red}2}{\color{Blue}e^{-\tau}}~d\tau} & {\color{Black}0<t<1} \\ | ||
| + | {\color{Black}\int_{{\color{Blue}0}}^{{\color{Red}t-1}}{\color{Red}1}{\color{Blue}e^{-\tau}}~d\tau} + | ||
| + | {\color{Black}\int_{{\color{Red}t-1}}^{{\color{Red}t}}{\color{Red}2}{\color{Blue}e^{-\tau}}~d\tau} & {\color{Black}1<t<3} | ||
| + | \end{cases} | ||
| + | \end{align} | ||
| + | </math></center> | ||
| + | <br clear=all> | ||
| + | === t>3 === | ||
| + | [[File:ConvDemo01p4.png|200px|thumb|right|Final overlap]] | ||
| + | Finally, once <math>t>3</math>, the trailing edge of the flipped <math>x</math> has passed the edge of <math>h</math> and the limits of integration are thus purely dependent on the piecewise boundaries of <math>x</math> alone: | ||
| + | <center><math> | ||
| + | \begin{align} | ||
| + | y(t)&=\begin{cases} {\color{Black}0} & {\color{Black}t<0} \\ | ||
| + | {\color{Black}\int_{{\color{Blue}0}}^{{\color{Red}t}}{\color{Red}2}{\color{Blue}e^{-\tau}}~d\tau} & {\color{Black}0<t<1} \\ | ||
| + | {\color{Black}\int_{{\color{Blue}0}}^{{\color{Red}t-1}}{\color{Red}1}{\color{Blue}e^{-\tau}}~d\tau} + | ||
| + | {\color{Black}\int_{{\color{Red}t-1}}^{{\color{Red}t}}{\color{Red}2}{\color{Blue}e^{-\tau}}~d\tau} & {\color{Black}1<t<3}\\ | ||
| + | {\color{Black}\int_{{\color{Red}t-3}}^{{\color{Red}t-1}}{\color{Red}1}{\color{Blue}e^{-\tau}}~d\tau} + | ||
| + | {\color{Black}\int_{{\color{Red}t-1}}^{{\color{Red}t}}{\color{Red}2}{\color{Blue}e^{-\tau}}~d\tau} & {\color{Black}t>3} | ||
| + | \end{cases} | ||
| + | \end{align} | ||
| + | </math></center> | ||
| + | <br clear=all> | ||
| + | === Animation of Flipped/Shifted x=== | ||
| + | Coming soon! | ||
| + | <!-- | ||
| + | Click this link to see an AVI movie of <math>h(t)</math> being flipped and shifted; you will likely want to right-click the link and open it in a new tab or window: [http://pundit.pratt.duke.edu/piki/images/f/f8/Peaks.avi Movie] | ||
| + | --> | ||
| + | |||
| + | == External References == | ||
| + | * Erik Cheever's [[https://github.com/echeever/ConvolveGUI Convolve GUI]] for MATLAB - an excellent way to visualize convolution using MATLAB | ||
| + | |||
| + | [[Category:ECE 280]] | ||
Latest revision as of 01:30, 17 September 2021
The following is an example of convolving two signals; the convolution is done several different ways:
- Math... So much math.
- Using Convolution Shortcuts
- Geometrically, flipping and shifting \(h(t)\)
- Geometrically, flipping and shifting \(x(t)\)
Contents
Setup
The goal for this problem is to determine the output \(y(t)\) created by an input \(x(t)\) for a linear time invariant system if the system's impulse response \(h(t)\) is known. In this particular example:
where the particular choice of which integral to use is up to the user.
Math
Given the relative complexity of \(x(t)\), it may make more sense to use the first form, where \(h(t)\) is flipped and shifted. That yields:
Distributing terms gives:
Taking the first part alone:
note that the integrand is only non-zero when two conditions are met simultaneously:
Furthermore, those conditions can only be met simultaneously if the outer conditions are met; that is, if:
These three conditions lead to three changes. The limits on \(\tau\) change the limits of the integral with respect to \(\tau\) while the condition on \(t\) can be represented by a unit step of \(t\). In other words:
Note with that last line that the integral is with respect to \(\tau\) and the exponent of \(\tau\) is +1. The other two components of the convolution integral can be processed in a similar way:
and
meaning (finally) that:
Written piecewise, this equation would be:
Shortcuts
Full color version:
To use the shortcuts, first distribute the various components of the convolution:
These can be rearranged, pulling out any shifts, as:
Note that each component now has a convolution of
in it. Convolution with a step generates an integral, and integrating the right-sided exponential yields:
which means the rearranged functions can be re-written as:
Now the shifts can be applied to give:
Black and white only:
To use the shortcuts, first distribute the various components of the convolution:
These can be rearranged, pulling out any shifts, as:
Note that each component now has a convolution of
in it. Convolution with a step generates an integral, and integrating the right-sided exponential yields:
which means the rearranged functions can be re-written as:
Now the shifts can be applied to give:
Geometrically Flipping/Shifting \(h\)
The geometric method involves determining the piecewise regions in \(\tau\) where the different functions overlap as a function of \(t\). With the current example, the only change \(h(t)\) makes is at \(t=0\), while \(x(t)\) has four different parts. The piecewise definitions of the two functions can be written as:
In the convolution integral
the piecewise definitions of the signals change to functions of \(\tau\):
As \(t\) changes, \(x(\tau)\) does not move but \(h(t-\tau)\) does, resulting in different components of the two functions overlapping at different times. The following four subsections will show what happens as \(t\) increases.
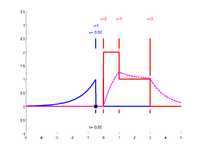
t<0
The "leading edge" of \(h(t-\tau)\) is at \(\tau=t\); until \(t>0\), there will be no overlap with \(x(\tau)\) and thus the convolution integral will be 0:
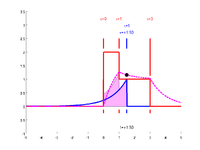
0<t<1
Once \(t>0\), the segment of \(h\) that is nonzero passes into the region of \(x\) that is equal to the constant 2. This will remain the situation until \(h\)'s transition into the region where \(x\) is 1. During this phase, the integrand will be the product of the exponential from \(h\) and the 2 from \(x\):
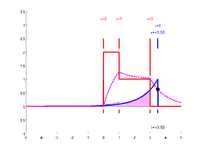
1<t<3
After \(t>1\) but before \(t>3\), there are two different regions of overlap: the region where \(x\) is 2 now overlaps for \(0<\tau<1\) while the region where \(x\) is 1 overlaps where \(1<\tau<t\). That yields:
t>3
Finally, once \(t>3\), the leading edge of the flipped \(h\) has passed the edge of \(x\) and the limits of integration are thus purely dependent on the piecewise boundaries of \(x\) alone:
After Integration
After calculating all those integrals, the answer would be:
or, combined,
Geometrically Flipping/Shifting x
The geometric method involves determining the piecewise regions in \(\tau\) where the different functions overlap as a function of \(t\). With the current example, the only change $h(t)$ makes is at \(t=0\), while \(x(t)\) has four different parts. The piecewise definitions of the two functions can be written as:
In the convolution integral
the piecewise definitions of the signals change to functions of \(\tau\):
As \(t\) changes, \(h(\tau)\) does not move but \(x(t-\tau)\) does, resulting in different components of the two functions overlapping at different times. The following four subsections will show what happens as \(t\) increases.
t<0
The "leading edge" of \(x(t-\tau)\) is at \(\tau=t\); until \(t>0\), there will be no overlap with \(h(\tau)\) and thus the convolution integral will be 0:
0<t<1
Once \(t>0\), the segment of \(x\) that is equal to the constant 2 passes into the region of \(h\) that is non-zero. This will remain the situation until \(x\)'s transition to the constant 1 passes into that region. During this phase, the integrand will be the product of the exponential from \(h\) and the 2 from \(x\):
1<t<3
After \(t>1\) but before \(t>3\), there are two different regions of overlap: the region where \(x\) is 1 now overlaps for \(0<\tau<t-1\) while the region where \(x\) is 2 overlaps where \(t-1<\tau<t-3\). That yields:
t>3
Finally, once \(t>3\), the trailing edge of the flipped \(x\) has passed the edge of \(h\) and the limits of integration are thus purely dependent on the piecewise boundaries of \(x\) alone:
Animation of Flipped/Shifted x
Coming soon!
External References
- Erik Cheever's [Convolve GUI] for MATLAB - an excellent way to visualize convolution using MATLAB
